Link Search Menu Expand Document

Partition by Values

Create complex partitions from multiple criteria

The Partition by Values node offer enhanced control over sub-group creation using multiple criteria, with rules specifying attributes for partitioning and optional pre-processing.

In
Points to break into partition
Partition Rules
Partition rules to be processed
Out
Partitioned points. If split output is enabled, outputs one point data per partition.

Table of content

Properties


Property Description
Settings
Split Output Whether to output individual partitions or simply write the unique partition key to an attribute.
Rules A list of ordered individual rules used for sorting the points.
Key Sum Outputs the sum of all partition keys to a int64 attribute.
This value is unlikely to be unique, but can come in handy for filtering purposes.
See Key Sum

Partition Rule

details/details-partition-rule.png

Property Description
Enabled Whether that rule is enabled or not. Helpful for trial and error without removing the configuration from the array.
Selector An attribute or property that will be used for partitioning. See .
Filter Size The size of the partition in relation the attribute or property uses.
Higher values means fewer larger partitions; smaller values means more smaller partitions.
Input pre-processing
Upscale A scale factor to apply to the selected attribute value before partitioning.
This is especially useful when working with smaller range of values like Density.
See Why upscale?.
Offset An offset value added to the selected attribute value before partitioning.
Offset is added to the Upscaled value.
This allow to shift separation ‘lines’ when using spatial values for partitioning.
Partition Key Attribute
Key Attribute Name Whether that rule is enabled or not. Helpful for trial and error without removing the configuration from the array.
Use Partition Index as Key Whether to use the partition Index as a key (starting at 0, up to N partitions) or the default output (actual under-the-hood value used to distinguish unique buckets).
See How partition Index works.
Partition Tagging
Only if Split Output is enabled
Tag Prefix Name Tag the data with the partition key, using the format Prefix::PartitionKey or Prefix::PartitionIndex
Tag Use Partition Index as Key Whether to use the partition Index as a key.
See How partition Index works.

When selecting a value to compare, keep in mind that it will be broadcasted to a double type. This means that if you don’t specify which component to use on multi-component type (Vectors, Transforms, etc), it will default to the first one (X).

Why upscale?

Under the hood, the Partition by Values broadcast and transform the reference values to a int64 used as a unique ID for individual partition.
Because of that, any value in the -1..1 range (such as Density, Steepness etc) will be rounded to the nearest integer.
Upscaling fixes this problem.

For example, without upscaling, [0.1, 0.25, 0.01] will be partitioned as [0, 0, 0]; so a unique 0-id’d partition.
On the other end, the same set [0.1, 0.25, 0.01] upscaled by a factor of 100 will be partitioned as [10, 25, 1]; so 3 separated partitions.

How partition Index works

The for each partition, the corresponding attribute value is basically upscaled, offsetted and rounded down. This operation is repeated for each partition rule, and points are then distributed into buckets which all have the same partition keys.
You can either output this “key” value as-is, or use the partition index. That index correspond to the partition order when all keys are sorted by ascending order.

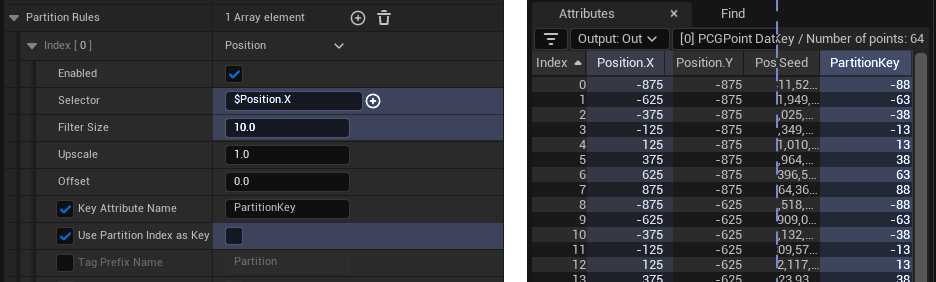
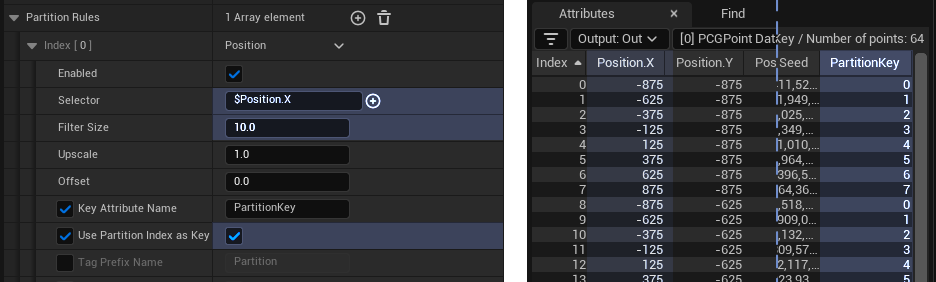
Using a single partition rule based on $Position.X, using a filter size of 10.
On the left is the detail panel, on the right is a screencap of the value debugger for that rule

Raw partition value


docs/partition/filtered.png

Index partition


docs/partition/index.png

Key Sum

The Key Sum attribute value will be, well, the sum of all unique partitions keys.
It’s useful in very specific scenarios, such as when partitioning based on booleans values, in order to filter partitions.

Say you have three separate boolean (or 0-1) attributes, with a partition rule set up for each of these attributes; with Use Partition Index as Key enabled.
Each partition will either have a 0 or 1 unique key, with a maximum of 9 partitions created (0 0 0, 1 0 0, 0 1 0 etc.). You will only have 4 different Key Sum: 0, 1, 2 and 3, which you can use as sort-of weak flag system:

  • 0 0 0 = 0
  • 1 0 0 = 1
  • 0 1 0 = 1
  • 0 0 1 = 1
  • 1 1 0 = 2
  • 0 1 1 = 2
  • 1 0 1 = 2
  • 1 1 1 = 3